Полярная звезда
2016
Составьте таблицу значений и постройте график функции, заданной формулой:
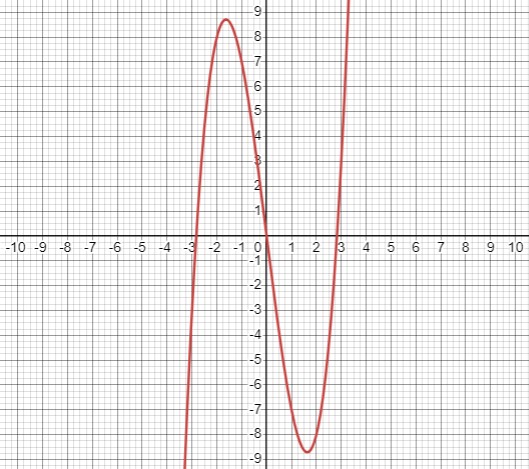
а) \(y=x^{3}-8 x\), где \(-3 \leq x \leq 3\);
б) \(y=\frac{4}{x+2}\), где \(-1,5 \leq x \leq 6\).
Каково множество значений функции?
а
Для поиска области значений функции \( y = x^2 - 9 \) используем таблицу значений:
\(\begin{array}c\hline y & -3 & -2 & -1 & 0 & 1 & 2 & 3 \\\hline x & -3 & 8 & 7 & 0 & -7 & -8 & 3 \\\hline\end{array}\)
Исходя из предоставленных значений, область значений - интервал \([-8.7 ; 8.7]\).
б
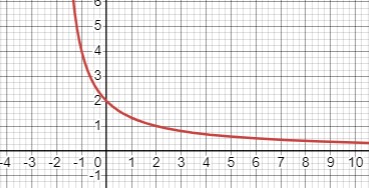
Для функции \( y = \frac{4}{x+2} \) проведена аналогичная таблица:
\(\begin{array}c\hline y & -1.5 & -1 & 0 & 1 & 2 & 3 & 4 & 5 & 6 \\\hline x & 8 & 4 & 2 & \frac{4}{3} & 1 & \frac{4}{5} & \frac{2}{3} & \frac{4}{7} & \frac{1}{2} \\\hline\end{array}\)
Область значений функции \( y = \frac{4}{x+2} \) - интервал \([0.5 ; 8]\).
Решебник
"Алгебра - Учебник" по предмету Алгебра за 8 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
Составьте таблицу значений и постройте график функции, заданной формулой: а) \(y=x^{3}-8 x\), где \(-3 \leq x \leq 3\); б) \(y=\frac{4}{x+2}\), где \(-1,5 \leq x \leq 6\). Каково множество значений функции?
Еще решебники за 8 класс
Мы подобрали сборники ГДЗ за 8 класс, которые могут быть Вам интересны.
