Вертикаль.
2015
При каких значениях \(x\) функция \(y=f(x)\) обращается в нуль, принимает положительные и отрицательные значения, если:
а) \(f(x)=-0,7 x+350\);
б) \(f(x)=30 x+10\)?
Начертите схематически график функции и проиллюстрируйте на нём установленные свойства.
а
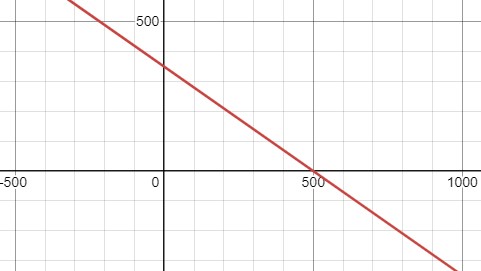
Для функции \( f(x) = -0.7x + 350 \):
Функция представляет собой прямую линию с коэффициентом наклона \( -0.7 \).
Нуль функции: \( -0.7x + 350 = 0 \), откуда \( x = 500 \).
Функция убывает: \( f(x) < 0 \) при \( x > 500 \), \( f(x) > 0 \) при \( x < 500 \).
б
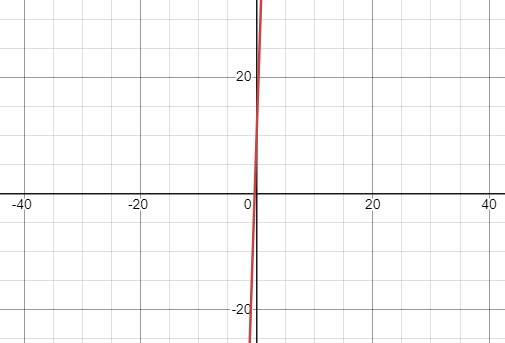
Для функции \( f(x) = 30x + 10 \):
Это также прямая линия с положительным коэффициентом наклона \( 30 \).
Нуль функции: \( 30x + 10 = 0 \), откуда \( x = -\frac{1}{3} \).
Функция возрастает: \( f(x) < 0 \) при \( x < -\frac{1}{3} \), \( f(x) > 0 \) при \( x > -\frac{1}{3} \).
Решебник
"Алгебра - Учебник" по предмету Алгебра за 8 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
При каких значениях \(x\) функция \(y=f(x)\) обращается в нуль, принимает положительные и отрицательные значения, если: а) \(f(x)=-0,7 x+350\); б) \(f(x)=30 x+10\)? Начертите схематически график функции и проиллюстрируйте на нём установленные свойства.
Еще решебники за 8 класс
Мы подобрали сборники ГДЗ за 8 класс, которые могут быть Вам интересны.
