Алгоритм успеха
2018
Постройте в одной системе координат в первой координатной четверти графики функций \(y=x, y=x^{2}, y=x^{3}, y=\sqrt{x}\).
a) Укажите координаты точек, которые являются общими для всех этих графиков.
б) Опишите взаимное расположение этих графиков на отрезке \([0; 1]\) и на луче \([1;+\infty)\).
в) Глядя на рисунок, расположите в порядке возрастания числа: \(0,37; 0,37^{2}; 0,37^{3}; \sqrt{0,37}\).
г) Расположите в порядке убывания числа: \(4,6; 4,6^{2}; 4,6^{3}\); \(\sqrt{4,6}\).
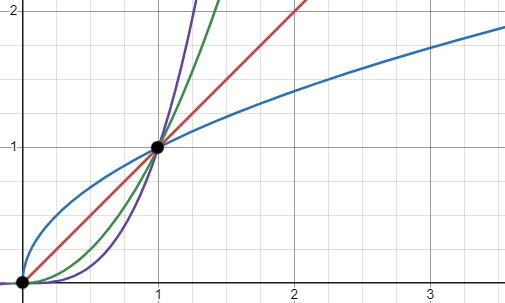
\(y=x\) красный
\(y=x^{2}\) зеленый
\(y=x^{3}\) фиолетовый
\( y=\sqrt{x}\) синий.
а
Точки \((0, 0)\) и \((1, 1)\) являются узлами графиков указанных функций.
б
На отрезке \([0, 1]\) функции упорядочены по возрастанию следующим образом: сначала идет функция \(y = \sqrt{x}\), затем \(y = x\), далее \(y = x^2\), и, наконец, самая нижняя функция \(y = x^3\). На луче \([1, +\infty)\) порядок функций меняется на обратный.
в
Проверка неравенств для числа \(0.37\) дает:
\(0.37^3 < 0.37^2 < 0.37 < \sqrt{0.37}\).
г
Аналогично, для числа \(4.6:\)
\(4.6^3 > 4.6^2 > 4.6 > \sqrt{4.6}\).
Решебник
"Алгебра - Учебник" по предмету Алгебра за 8 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
Постройте в одной системе координат в первой координатной четверти графики функций \(y=x, y=x^{2}, y=x^{3}, y=\sqrt{x}\). a) Укажите координаты точек, которые являются общими для всех этих графиков. б) Опишите взаимное расположение этих графиков на отрезке \([0; 1]\) и на луче \([1;+\infty)\). в) Глядя на рисунок, расположите в порядке возрастания числа: \(0,37; 0,37^{2}; 0,37^{3}; \sqrt{0,37}\). г) Расположите в порядке убывания числа: \(4,6; 4,6^{2}; 4,6^{3}\); \(\sqrt{4,6}\).
Еще решебники за 8 класс
Мы подобрали сборники ГДЗ за 8 класс, которые могут быть Вам интересны.
