Сфера жизни
2015
Дана функция
\(y=\begin{cases}x^{-1}, \text { если } x<-\frac{1}{2}, \\4 x, \text { если }-\frac{1}{2} \leq x \leq \frac{1}{2}, \\x^{-1}, \text { если } x>\frac{1}{2} .\end{cases}\)
Сколько корней имеет уравнение:
a) \(y=2\);
б) \(y=\frac{1}{3}\);
в) \(y=0\);
г) \(y=-3\)?
У нас дана функция, которая определена разными областями для разных значений \(x\):
1. Для \(x < -\frac{1}{2}\): \(y = x^{-1}\).
2. Для \(-\frac{1}{2} \leq x \leq \frac{1}{2}\): \(y = 4x\).
3. Для \(x > \frac{1}{2}\): \(y = x^{-1}\)
а
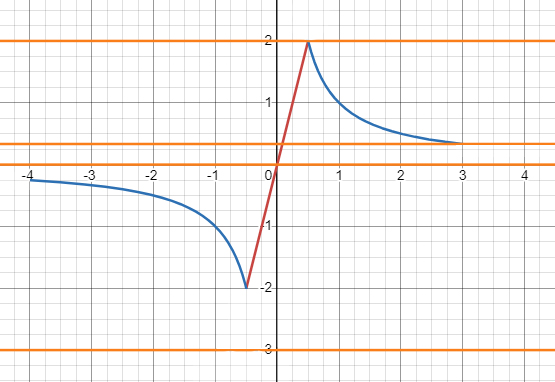
Если \(y = 2\), то есть 1 корень, так как функция \(y = 4x\) пересекается с линией \(y = 2\) при \(x = \frac{1}{2}\).
б
Если \(y = \frac{1}{3}\), то есть 2 корня, так как функции \(y = x^{-1}\) и \(y = 4x\) пересекаются при двух точках.
в
Если \(y = 0\), то есть 1 корень, так как функция \(y = 4x\) пересекается с осью \(x\) при \(x = 0\).
г
Если \(y = -3\), то нет корней, так как нет значения \(x\), для которого функция принимает значение \(-3\).
Решебник
"Алгебра - Учебник" по предмету Алгебра за 8 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
Дана функция \(y=\begin{cases}x^{-1}, \text { если } x<-\frac{1}{2}, \\4 x, \text { если }-\frac{1}{2} \leq x \leq \frac{1}{2}, \\x^{-1}, \text { если } x>\frac{1}{2} .\end{cases}\) Сколько корней имеет уравнение: a) \(y=2\); б) \(y=\frac{1}{3}\); в) \(y=0\); г) \(y=-3\)?
Еще решебники за 8 класс
Мы подобрали сборники ГДЗ за 8 класс, которые могут быть Вам интересны.
