Вертикаль
2018
(Для работы в парах.) Проиллюстрируйте с помощью кругов Эйлера соотношение между множествами \(A\) и \(B\) и найдите пересечение и объединение этих множеств, если:
a) \(A\) - множество целых чисел, кратных \(3, B\) - множество целых чисел, кратных 5;
б) \(A\) - множество целых чисел, кратных \(3, B\) - множество целых чисел, кратных 15.
1) Распределите, кто выполняет задания для случая а), а кто для случая б), и выполните их.
2) Проверьте друг у друга, верно ли выполнен рисунок и правильно ли найдены пересечение и объединение множеств \(A\) и \(B\).
3) Исправьте ошибки, если они допущены.
а
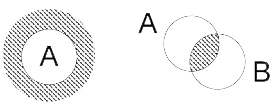
Первый рисунок
\(\mathrm{A} \cap \mathrm{B}\) - множество целых чисел, кратных 15
\(\mathrm{A} \cup \mathrm{B}\) - множество целых чисел, кратных 3 или 5.
б
Второй рисунок
\(\mathrm{A} \cap \mathrm{B}=\mathrm{B}\) - множество целых чисел, кратных 3
\(\mathrm{A} \cup \mathrm{B}=\mathrm{A}-\) множество целых чисел, кратных 15.
Решебник
"Алгебра - Учебник" по предмету Алгебра за 8 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
(Для работы в парах.) Проиллюстрируйте с помощью кругов Эйлера соотношение между множествами \(A\) и \(B\) и найдите пересечение и объединение этих множеств, если: a) \(A\) - множество целых чисел, кратных \(3, B\) - множество целых чисел, кратных 5; б) \(A\) - множество целых чисел, кратных \(3, B\) - множество целых чисел, кратных 15. 1) Распределите, кто выполняет задания для случая а), а кто для случая б), и выполните их. 2) Проверьте друг у друга, верно ли выполнен рисунок и правильно ли найдены пересечение и объединение множеств \(A\) и \(B\). 3) Исправьте ошибки, если они допущены.
Еще решебники за 8 класс
Мы подобрали сборники ГДЗ за 8 класс, которые могут быть Вам интересны.
