Физика
2023
(Задача-исследование.) Изменение температуры воды \(p({ }^{\circ} \mathrm{C})\) в баке как функции времени \(t\) (мин) описано с помощью формулы:
\(p=\begin{cases}2 t+20, \text { если } 0 \leq t<40, \\ 100, \text { если } 40 \leq t \leq 60, \\ -\frac{2}{3} t+140, \text { если } 60<t \leq 150\end{cases}\).
1) Определите, как изменялась температура воды в каждом из указанных промежутков времени.
2) Постройте график функции \(p=f(t)\).
3 ) Обсудите, какой физический смысл имеет процесс, описанный функцией \(p=f(t)\), в каждом из промежутков времени \([0; 40);[40; 60];(60; 150]\).
Из предоставленной информации можно сделать следующие выводы:
1
Изначально: Температура воды поднялась с 20 до 100 градусов.
Далее: В течение некоторого времени температура держалась на уровне 100 градусов.
После этого: Температура воды начала снижаться и достигла 40 градусов.
2
3
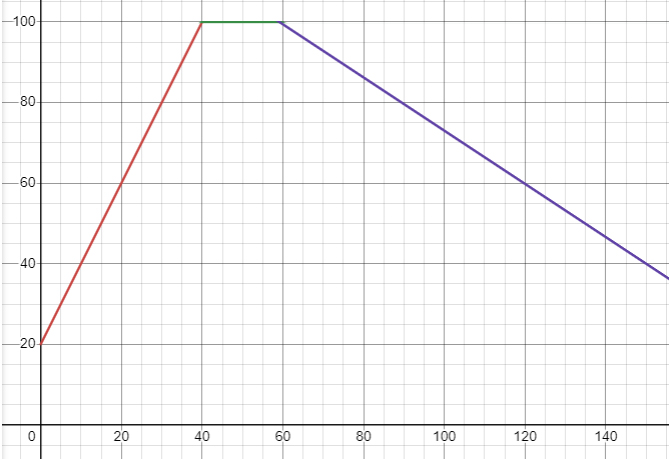
При \(t \in [0; 40):\) Вода нагревается.
При \(t \in [40; 60]:\) Вода кипит, и температура остается неизменной.
При \(t \in (60; 150]:\) Вода остывает.
Решебник
"Алгебра - Учебник" по предмету Алгебра за 8 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
(Задача-исследование.) Изменение температуры воды \(p({ }^{\circ} \mathrm{C})\) в баке как функции времени \(t\) (мин) описано с помощью формулы: \(p=\begin{cases}2 t+20, \text { если } 0 \leq t<40, \\ 100, \text { если } 40 \leq t \leq 60, \\ -\frac{2}{3} t+140, \text { если } 60<t \leq 150\end{cases}\). 1) Определите, как изменялась температура воды в каждом из указанных промежутков времени. 2) Постройте график функции \(p=f(t)\). 3 ) Обсудите, какой физический смысл имеет процесс, описанный функцией \(p=f(t)\), в каждом из промежутков времени \([0; 40);[40; 60];(60; 150]\).
Еще решебники за 8 класс
Мы подобрали сборники ГДЗ за 8 класс, которые могут быть Вам интересны.
