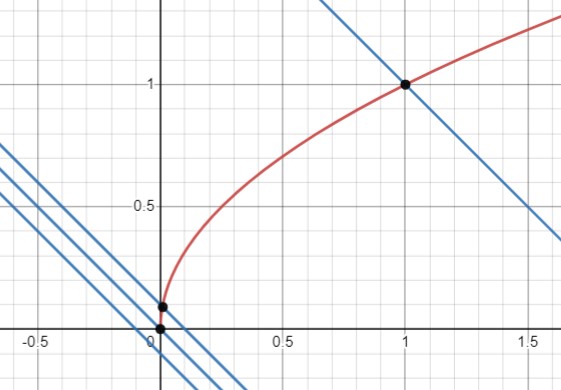
Какой из графиков линейных функций не пересекает графика функции \(y=\sqrt{x}\)?
1. \(y=-x+2\)
2. \(y=-x\)
3. \(y=-x+0,1\)
4. \(y=-x-0,1\)
Для того чтобы найти, какой из графиков линейных функций не пересекается с графиком функции \(y = \sqrt{x}\), нужно рассмотреть условие, при котором \(y\) (график линейной функции) меньше или равно \(\sqrt{x}\) для всех значений \(x\).
График функции \(y = \sqrt{x}\) представляет собой положительный корень из \(x\) и начинается в начале координат (0,0) и растет при увеличении \(x\).
Теперь рассмотрим уравнения линейных функций:
1. \(y = -x + 2\) - график с отрицательным наклоном и положительным сдвигом. Он пересекается с графиком \(\sqrt{x}\).
2. \(y = -x\) - график с отрицательным наклоном, проходящий через начало координат. Он также пересекается с графиком \(\sqrt{x}\).
3. \(y = -x + 0,1\) - аналогично, график с отрицательным наклоном и положительным сдвигом. Он пересекается с графиком \(\sqrt{x}\).
4. \(y = -x - 0,1\) - график с отрицательным наклоном и отрицательным сдвигом. Этот график будет ниже графика \(\sqrt{x}\) при всех значениях \(x\), таким образом, он не пересекается с графиком \(\sqrt{x}\).
Итак, линейная функция \(y = -x - 0,1\) не пересекается с графиком функции \(y = \sqrt{x}\).
Решебник
"Алгебра - Учебник" по предмету Алгебра за 8 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
Какой из графиков линейных функций не пересекает графика функции \(y=\sqrt{x}\)? 1. \(y=-x+2\) 2. \(y=-x\) 3. \(y=-x+0,1\) 4. \(y=-x-0,1\)

