История России.
2017
Решите уравнение \(x^{2}=0,5 x+3\) сначала графически, а затем с помощью формулы корней.
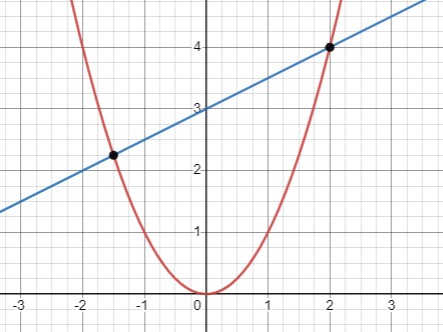
Аналитическое решение:
Уравнение \(x^2 - 0.5x - 3 = 0:\)
Вычисляем дискриминант: \(D = (0.5)^2 - 4 \cdot 1 \cdot (-3) = 12.25 = 3.5^2\).
Находим корни: \(x = \frac{0.5 \pm 3.5}{2}\).
Итак, \(x_1 = -1.5\), \(x_2 = 2\).
Решебник
"Алгебра - Учебник" по предмету Алгебра за 8 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
Решите уравнение \(x^{2}=0,5 x+3\) сначала графически, а затем с помощью формулы корней.
Еще решебники за 8 класс
Мы подобрали сборники ГДЗ за 8 класс, которые могут быть Вам интересны.
