Дополнительные упражнения к главе V — К параграфу 14 — 1164 — стр. 259

Первая функция: \(y= \begin{cases}x^{2}, \text { если } x \leq 1 \\ \sqrt{x}, \text { если } x>1;\end{cases}\)

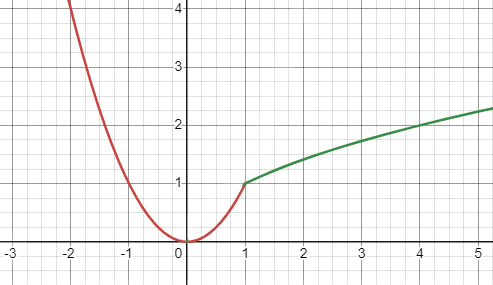
Функция определена для всех действительных чисел, следовательно, область определения \( D(y) \) составляет \((-\infty, +\infty)\).

Функция принимает только неотрицательные значения, так как является квадратом, а квадрат любого числа неотрицателен. Область значений \( E(y) \) - \((0, +\infty)\).

У функции есть нулевая точка в \( x = 0 \).

Функция убывает при \( x \in (-\infty, 0] \) и возрастает при \( x \in [0, +\infty)\).

Вторая функция: \(y=\begin{cases}(x-1)^{2}, \text { если } x \leq 2, \\ -2 x+5, \text { если } 2<x \leq 3\end{cases}\)

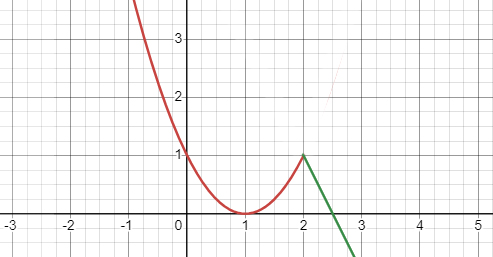
Область определения \( D(y) \) ограничена \((-\infty, 3]\), так как первая часть определена для \( x \leq 2 \), а вторая для \( 2 < x \leq 3 \).

Область значений \( E(y) \) - \([-1, +\infty)\).

Нули функции находятся в \( x = 1 \) и \( x = 2.5 \).

Функция убывает на интервалах \( (-\infty, 1] \cup [2, 3] \) и возрастает на \( [1, 2] \).