§7. Уравнения с двумя перемннными и их системы — 20. Решение систем уравнений с двумя переменными — 399 — стр. 122

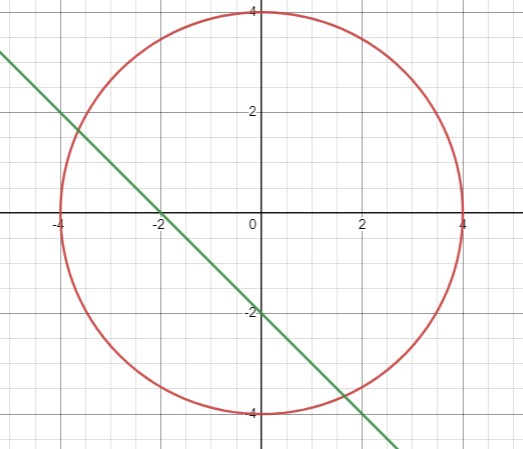
Рассмотрим систему уравнений:

\(\begin{cases}x^2+y^2=16 \\x+y+2=0\end{cases}\)

Выразим одну переменную через другую из второго уравнения:

\(y = -x - 2\)

Подставим это выражение в первое уравнение:

\(x^2 + (-x-2)^2 = 16\)

Решив уравнение, получаем два решения:

\(\{(-3.65, 1.65),(1.65, -3.65)\}\).

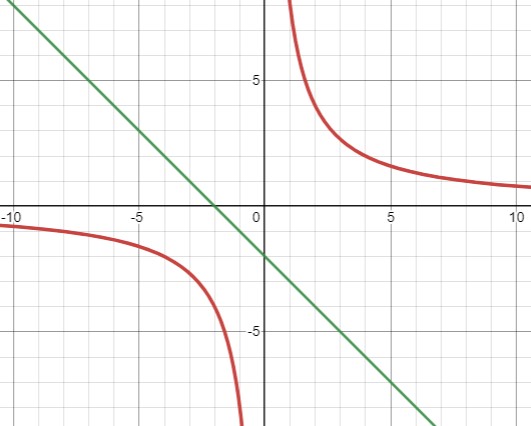
Рассмотрим систему уравнений:

\(\begin{cases}xy = 8 \\x+y+3 = 0\end{cases}\Leftrightarrow \begin{cases}y=\frac{8}{x} \\x+y=-3\end{cases}\)

Так как второе уравнение не имеет решений при данных условиях, система не имеет решений.

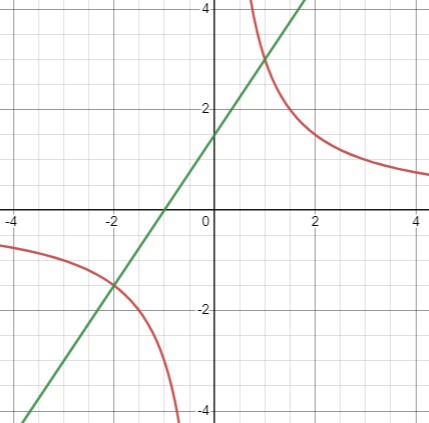
Рассмотрим систему уравнений:

\(\begin{cases}xy - 3 = 0 \\2y - 3x = 3\end{cases}\Leftrightarrow \begin{cases}y=\frac{3}{x} \\2y-3x=3\end{cases}\)

Решив систему, получаем два решения:

\(\{(-2, -1.5), (1, 3)\}\).

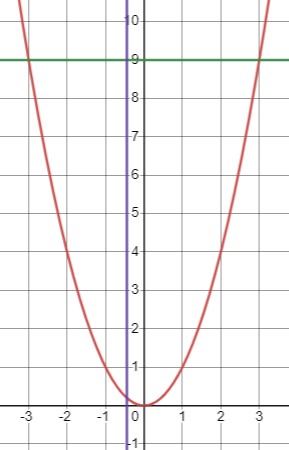
Рассмотрим систему уравнений:

\(\begin{cases}x^2 - y = 0 \\(9x+4)(y-9) = 0\end{cases}\Leftrightarrow \begin{cases}y=x^2 \\{\begin{cases}x=-\frac{4}{9} \\y=9\end{cases}}\end{cases}\)

Таким образом, система имеет три решения:

\(\left\{(-3, 9), (3, 9), \left(-\frac{4}{9}, \frac{16}{81}\right)\right\}\).