§7. Уравнения с двумя перемннными и их системы — 20. Решение систем уравнений с двумя переменными — 402 — стр. 123

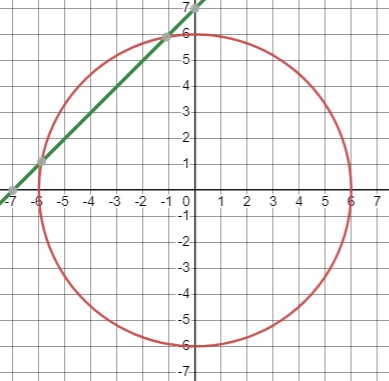
Графическое решение:

Система представляет собой окружность с центром в начале координат и радиусом 6 и прямую с наклоном 45 градусов, проходящую через точку (-7, 0). Точки пересечения этих графиков дают решения системы.

Два решения графически обозначают точки:

\(\{(-5.9, 1.1), (-1.1, 5.9)\}\).

Аналитическое решение:

Преобразуем систему уравнений:

\( \begin{cases}x^2+(x+7)^2=36 \\y=x+7\end{cases} \\ x^2+x^2+14x+49=36 \\ 2x^2+14x+13=0\)

Вычислим дискриминант:

\(D=14^2-4 \cdot 2 \cdot 13=196-104=92\)

Найдем значения переменных:

\(x=\frac{-14 \pm 2 \sqrt{23}}{4}=\frac{-7 \pm \sqrt{23}}{2}\)

Подставим найденные значения \(x\) в уравнение \(y=x+7\) и получим соответствующие значения \(y\).

Таким образом, два аналитических решения системы:

\(\left\{\left(\frac{-7-\sqrt{23}}{2}, \frac{7-\sqrt{23}}{2}\right), \left(\frac{-7+\sqrt{23}}{2}, \frac{7+\sqrt{23}}{2}\right)\right\}\).