§7. Уравнения с двумя перемннными и их системы — 20. Решение систем уравнений с двумя переменными — 403 — стр. 123

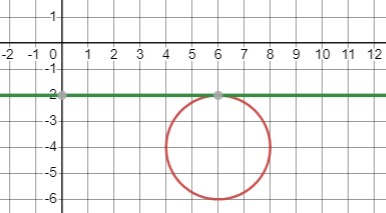
Рассмотрим систему уравнений:

\(\begin{cases}(x-6)^2+(y+4)^2=4 \\y=-2\end{cases}\)

Это уравнение окружности с центром в точке \((6, -4)\) и радиусом 2, а также горизонтальная прямая \(y=-2\). Точка пересечения этих графиков будет единственным решением системы.

Одна общая точка:

\(\{ (6, -2) \}\).

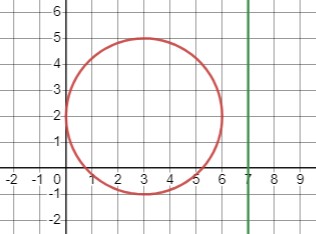
Теперь рассмотрим систему уравнений:

\(\begin{cases}(x-3)^2+(y-2)^2=9 \\x=7\end{cases}\)

Это уравнение окружности с центром в точке \((3, 2)\) и радиусом 3, а также вертикальная прямая \(x=7\). Эти графики не пересекаются, поэтому система не имеет общих точек.

Нет общих точек.