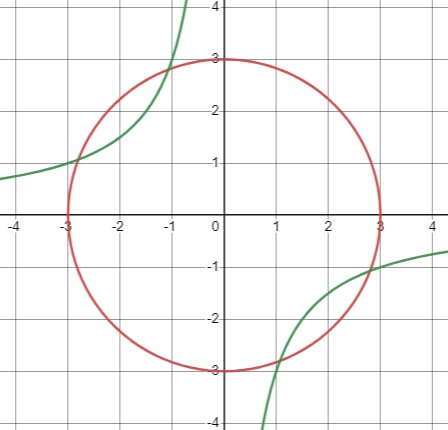
Пересекаются ли окружность \(x^{2}+y^{2}=9\) и гипербола \(xy=-3\) ? Если пересекаются, то сколько общих точек они имеют?
Рассмотрим систему уравнений:
\(\begin{cases}x^{2}+y^{2}=9 \\x y=3\end{cases}\)
Первое уравнение представляет собой уравнение окружности с центром в начале координат и радиусом 3. Второе уравнение описывает гиперболу, которая пересекается с окружностью в четырех точках.
4 общие точки.
Решебник
"Алгебра - Учебник" по предмету Математика за 9 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
Пересекаются ли окружность \(x^{2}+y^{2}=9\) и гипербола \(xy=-3\) ? Если пересекаются, то сколько общих точек они имеют?

