Докажите, что графики функций \(y=\sqrt{x}\) и \(y=x+0,5\) не имеют общих точек.
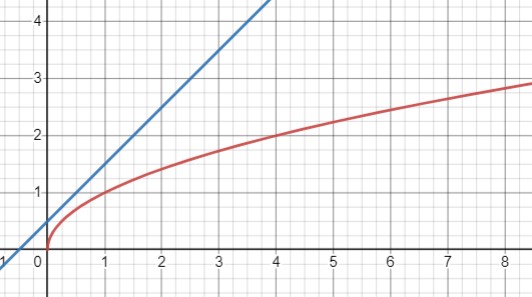
Мы начинаем с уравнения \( \sqrt{x} = x + 0,5 \) для нахождения точек пересечения двух функций.
Далее, мы возводим обе стороны уравнения в квадрат, получая \( x = (x + 0,5)^2 = x^2 + x + 0,25 \).
Получаем квадратное уравнение \( x^2 + 0,25 = 0 \).
При попытке найти корни этого уравнения, мы видим, что \( x^2 = -0,25 \). Однако отрицательный радикал не имеет действительных корней.
Таким образом, уравнение не имеет действительных корней, что означает, что графики не имеют общих точек.
Решебник
"Алгебра - Учебник" по предмету Алгебра за 8 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
Докажите, что графики функций \(y=\sqrt{x}\) и \(y=x+0,5\) не имеют общих точек.

