Постройте график уравнения:
a) \(y-x^{2}=0\);
б) \(y-x^{3}=0\);
в) \(0,5 x y+1,5=0\);
г) \(y+x^{3}=0\).
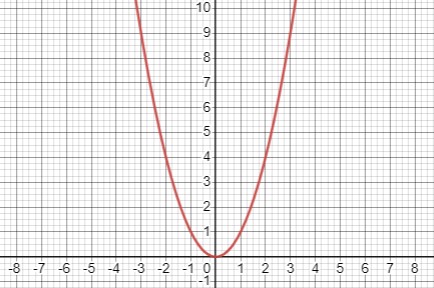
Уравнение \(y - x^2 = 0\) описывает параболу \(y = x^2\). Мы строим ее, зная, что коэффициент \(a = 1 > 0\), что означает, что ветви параболы направлены вверх. Функция является четной, что подтверждается условием \(y(-x) = y(x)\).
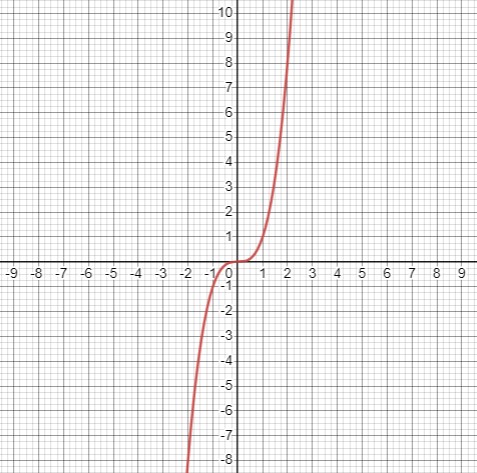
Уравнение \(y - x^3 = 0\) представляет собой кубическую параболу \(y = x^3\). Коэффициент \(a = 1 > 0\), парабола лежит в 1 и 3 четвертях. Функция нечетная \(y(-x) = -y(x))\). Cтроим правую ветвь и отображаем относительно начала координат.
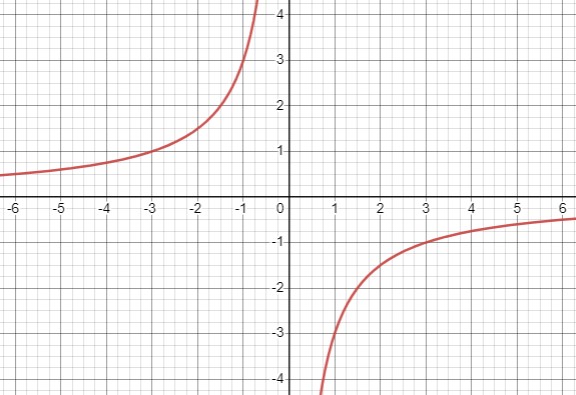
Уравнение \(0.5xy + 1.5 = 0\) приводится к \(xy = -3\), хатем к \(y = -\frac{3}{x}\). Мы видим гиперболу с коэффициентом \(k = -3 < 0\), она лежит во 2 и 4 четвертях. Функция нечетная \(y(-x) = -y(x)\). Строим левую ветвь и отображаем относительно начала координат.
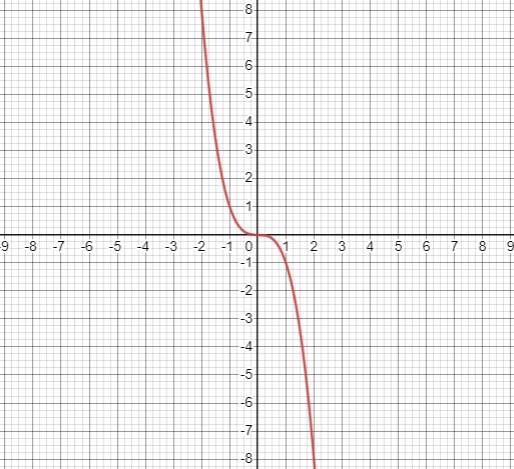
Уравнение \(y + x^3 = 0\) дает \(y = -x^3\), то есть кубическую параболу. Коэффициент \(a = -1 < 0\), лежит во 2 и 4 четвертях. Функция нечетная \(y(-x) = -y(x)\). Мы строим левую ветвь и отображаем относительно начала координат.
Решебник
"Алгебра - Учебник" по предмету Алгебра за 8 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
Постройте график уравнения: a) \(y-x^{2}=0\); б) \(y-x^{3}=0\); в) \(0,5 x y+1,5=0\); г) \(y+x^{3}=0\).

