Найдите область определения функции и постройте её график:
а) \(y=\frac{x^{2}-9}{6+2 x}\);
б) \(y=\frac{4-x^{2}}{x^{2}+2 x}\).
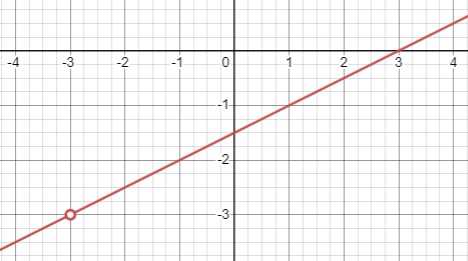
Уравнение: \(y = \frac{x^2 - 9}{6 + 2x}\)
Для того чтобы дробь была определена, знаменатель не должен быть равен нулю, то есть \(6 + 2x \neq 0\). Отсюда следует, что \(x \neq -3\).
Область допустимых значений: \(D(y) = (-\infty, -3) \cup (-3, +\infty)\).
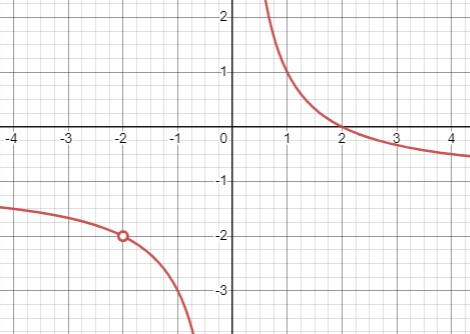
Уравнение: \(y = \frac{4 - x^2}{x^2 + 2x} = \frac{(2 - x)(2 + x)}{x(x + 2)} = \frac{2 - x}{x}\)
Чтобы дробь была определена, знаменатель не должен быть равен нулю, а также не должен быть равен -2. Таким образом, \(x \neq 0\) и \(x \neq -2\).
Область допустимых значений: \(D(y) = (-\infty, -2) \cup (-2, 0) \cup (0, +\infty)\).
Решебник
"Алгебра - Учебник" по предмету Алгебра за 8 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
Найдите область определения функции и постройте её график: а) \(y=\frac{x^{2}-9}{6+2 x}\); б) \(y=\frac{4-x^{2}}{x^{2}+2 x}\).

