Полярная звезда
2016
Постройте график функции
\(y=\begin{cases}x^{-2}, \text { если }-2 \leq x<-1, \\x^{2}, \text { если }-1 \leq x \leq 1, \\x^{-2}, \text { если } 1<x \leq 2 \end{cases}\)
Сколько общих точек имеет этот график с прямой \(y=a\) в случае, когда:
a) \(a=2\);
б) \(a=1\);
в) \(a=\frac{1}{2}\);
г) \(a=0\)?
а
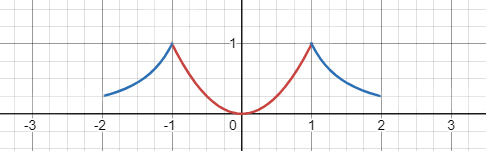
Если \(y = 2\), то нет общих точек, так как ни одна из функций не принимает значение 2.
б
Если \(y = 1\), то есть 2 общие точки, так как функции \(y = x^2\) и \(y = x^{-2}\) пересекаются при \(x = -1\) и \(x = 1\).
в
Если \(y = \frac{1}{2}\), то есть 4 общие точки, так как у каждой из функций две точки, где они пересекаются с прямой \(y = \frac{1}{2}\).
г
Если \(y = 0\), то есть 1 общая точка, так как область значений функции \(y = x^2\) включает 0, и есть только одна точка, где \(x = 0\).
Решебник
"Алгебра - Учебник" по предмету Алгебра за 8 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
Постройте график функции \(y=\begin{cases}x^{-2}, \text { если }-2 \leq x<-1, \\x^{2}, \text { если }-1 \leq x \leq 1, \\x^{-2}, \text { если } 1<x \leq 2 \end{cases}\) Сколько общих точек имеет этот график с прямой \(y=a\) в случае, когда: a) \(a=2\); б) \(a=1\); в) \(a=\frac{1}{2}\); г) \(a=0\)?
Еще решебники за 8 класс
Мы подобрали сборники ГДЗ за 8 класс, которые могут быть Вам интересны.
